Lesson Design Principles

Skew The Script uses the following design principles as a rubric for lesson creation and evaluation. Although none of our lessons perfectly satisfy every design principle, the principles serve as our guidepost for expanding and improving our curriculum.

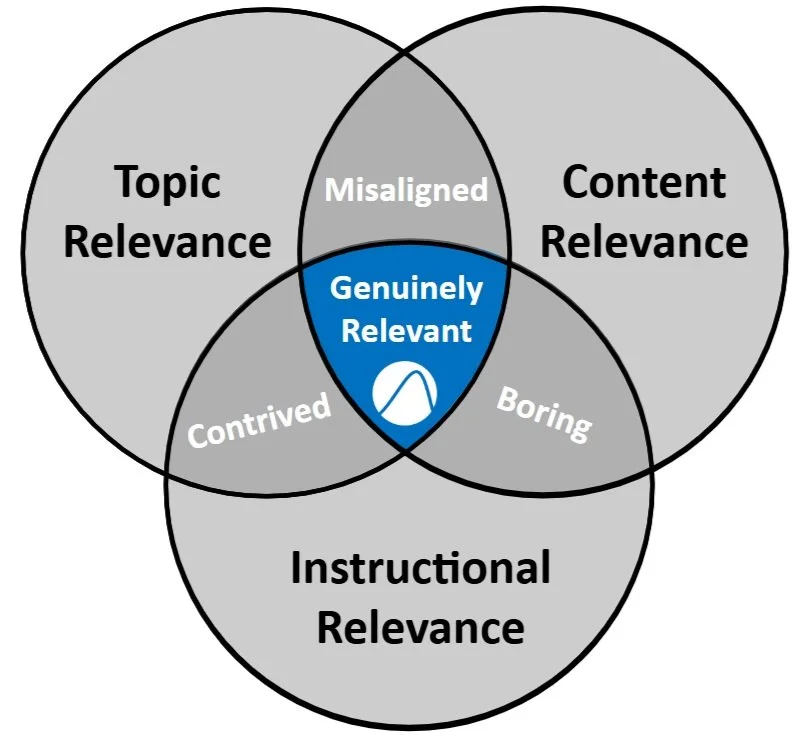
1) Our lessons make math what it already is: Relevant.

Specifically, our lessons meet the three criteria for relevance:

Topic Relevance: The context is compelling

The lessons explore contexts that are authentically meaningful, compelling, and important to students’ lives.

  • To engage all students, we can’t make the promise that math will, at some point in the vague future, be relevant. Especially for students who work jobs outside of school, support their families, and manage complex problems on a regular basis, this vague promise can feel like an empty one. The math needs to be helpful, useful, and relevant now. Relevant contexts make these connections current and clear.

Content Relevance: The math is essential

The math isn’t a side-show or veneer. Rather, the math is central, and it provides genuine insight into the context.

  • Students should walk away feeling that the math skills they learned were essential for understanding key aspects of the lesson context. Otherwise, while the context may have been relevant, the math used in the lesson will continue to feel like an irrelevant add-on.

Instructional Relevance: The material is instructionally useful

The lessons fit into teachers’ calendars, are aligned to math standards, and prepare students for the assessments they need to take.

  • Math teachers have a short amount of time to cover all the standards for their courses. In addition, for many courses, they have to prepare students for standardized tests. To be useful under these conditions, lessons must be created in well-chunked formats. They must be aligned to course standards. Finally, they must genuinely prepare students for the exams they need to take.

Problems that lack topic relevance -> Boring

Boring Problem: A factory claims that its batteries can recharge in 60 minutes, on average. To test this claim, a statistician gets a random sample of 30 batteries and finds that they take an average of 67 minutes to recharge. Is there convincing statistical evidence that true average recharge time is longer than claimed?

Analysis: This problem sets up a one-sample t-test for a mean, which is a mathematical process that gives students genuine insight into whether the factory’s claim is true. However, the overall context (battery lifetimes) isn’t compelling. The problem is missing topic relevance. It’s boring.

  • ❌ Topic Relevance
  • ✅ Content Relevance
  • ✅ Instructional Relevance

Problems that lack content relevance -> Contrived

Contrived Problem: On any given day, there is a 10% chance that a citizen of Wakanda will require the help of the Black Panther. In a full year, how many days would we expect T’Challa to suit up and save someone?

Analysis: Some students love the Black Panther. However, solving this proportions/expected value problem (with made-up numbers) does not give students genuine insight into the storylines, character, and contexts that they love about the Black Panther. Because the math content doesn’t provide real insight into the context, it feels contrived. The Black Panther becomes a disingenuous “veneer of relevance” on top of a standard math problem.

  • ✅ Topic Relevance
  • ❌ Content Relevance
  • ✅ Instructional Relevance

Problems that lack instructional relevance -> Misaligned

Misaligned Problem: Many assume that electric cars are better for the planet. However, the precious metals in batteries make electric cars quite emissions-heavy to produce. When you consider the full life of a car, does going electric actually reduce emissions? According to MIT's Trancik Lab dataset, re-charging a Telsa typically requires 1,368 kg CO2eq (emissions equivalent to 1,368 kg of CO2) from electric grids per year of driving. By contrast, a Toyota Camry emits far more: 4,525 kg CO2eq per year of driving. However, it takes far more emissions to produce a Tesla (11,074 kg CO2eq for a Tesla vs 7,402 for a Camry). How long do you have to drive the Tesla for it to 'pay off?' Construct a system and solve using elimination.

Analysis: With proper framing, the question of whether electric cars are actually better for the environment is compelling for students. The problem requires students to set up equations like these:

Where 𝑦 = total emissions and 𝑥 = years driven
Tesla: 𝑦 = 1368𝑥 + 11074
Camry: 𝑦 = 4525𝑥 + 7402

Solving this system using elimination would give students genuine insight into the context, as the solution reveals that it only takes 1.16 years of driving for the Tesla to have lower overall emissions. So, barring a car-totalling accident in the first year of driving, going electric (in this case) tends to pay off! However, standardized tests usually assess whether students can use elimination to solve a system of standard form equations. These equations are in y-intercept form. Solving these equations with elimination won't prepare students for the level of algebraic manipulation needed to solve standard form equations. So, this problem is not instructionally useful.

  • ✅ Topic Relevance
  • ✅ Content Relevance
  • ❌ Instructional Relevance

How do we meet all 3 relevance criteria? Using the Students First, Standards Last Method

In the typical curriculum creation process, lesson designers start with the math standards they need to cover. Then, they fit their lesson contexts and tasks to those standards. The result: lessons that are well-aligned to standards (Instructional Relevance) but with either boring contexts that lack Topic Relevance or contrived connections that lack Content Relevance.

Skew The Script takes an inverted approach. We consider the math standards last. That’s not to say that the math standards aren’t important - far from it! We believe that designing lessons aligned to math standards - and to the way those standards are tested - is essential. Otherwise, the lessons would lack Instructional Relevance and would be useless for most classrooms.

While not last in importance, math standards are saved for the last step of our creation process. We start at a very different place: asking students what they care about (Topic Relevance). Then, we see what math naturally surfaces when we start exploring those student-chosen contexts (Content Relevance). This ordering ensures that our lessons investigate compelling contexts, using math that genuinely fits those contexts. Finally, when choosing which ideas to build into full lessons, we only select those that utilized common math concepts from high school courses (Instructional Relevance). In this way, we ensure that all 3 relevance criteria are satisfied.

2) Our lessons use contexts that endure over time.

Math lessons can temporarily satisfy the three criteria for relevance (Topic Relevance, Content Relevance, Instructional Relevance) during one school year.  However, when taught the next school year, the relevance fades. This can happen when the lesson…

  • Centers on a current event that’s no longer “current” or compelling at a later date (loses Topic Relevance)

  • Depends on mathematical patterns in old data that are no longer present in current data (loses Content Relevance)

  • Covers math standards in ways that don’t align well to new assessments (loses Instructional Relevance)

Although no lesson will ever be permanently relevant, lessons should be designed to have their relevance endure for as many school years as possible. Using lessons across school years allows instructors to hone their implementation of lessons, while also reducing their prep burden. In addition, it gives lesson designers the capacity to expand lesson offerings, without having to continually redesign old lessons.

For these reasons, Skew The Script frames its lessons around enduring key questions (e.g. “Does college pay off?”) rather than temporary current events (e.g. “Why did the Covid-19 pandemic lead to high inflation of the dollar?”). This allows us to regularly update the lessons with new figures and data over time (e.g. updating the estimate for average college costs to reflect the most recent data) without having to change the overall structure/theme of the lesson. In addition, we regularly review the structure of questions on standardized tests (e.g. AP Exams) to ensure our lessons prepare students for the questions they’ll face on current assessments.

3) Our lessons are nonpartisan.

With more data at our fingertips than ever before, talking about civic issues often involves talking about math. At the same time, biased samples, correlation/causation fallacies, misleading denominators, and weak quantitative arguments appear almost everywhere we turn. It’s up to us to develop students’ civic math reasoning so that, as citizens, they’re prepared to discern the well-evidenced claims from a sea of misguided conclusions.

To develop students’ civic math reasoning, we invite real-world issues into the math classroom. Then, we ground the discussion in the scrupulous and common language of math. This orientation towards math instruction doesn’t mean teaching with a political bias. In fact, it’s the opposite: it prepares students to think critically, evaluate contrasting claims, and identify bias through mathematical analysis. The goal of every lesson is to heighten students’ discourse and reasoning - not to impose beliefs upon them.

We believe that the most rigorous, feasible, and valuable approach to teaching civic math reasoning is to ensure that lesson materials are nonpartisan. Our lessons are designed to ask open questions, challenge weak arguments, and allow students to come to their own conclusions through rigorous reasoning. We consistently seek to represent multiple perspectives (that are consistent with quantitative evidence) in the lesson materials. For example, in the first Skew The Script AP Statistics lesson, students analyze misleading data graphics from both Republican and Democratic politicians. In the Skew The Script data projects, you’ll find rigorously compiled economic data from the right-leaning Heritage Foundation, from the nonpartisan Tax Foundation, and from a left-leaning Harvard economist. Students critically analyze these datasets, their sources, and their implications. Finally, our lesson design process provides external checks of our internal biases. All lessons are reviewed by an experienced committee of politically diverse math teachers, to vet the materials for fairness, balance, and rigor. 

4) Our lessons respect teacher expertise and agency.

Skew The Script was started by teachers who created their own content, after finding that traditional lesson materials didn’t match the needs, desires, or interests of their students. Our organization wouldn’t exist if teachers didn’t have the expertise and agency to make curriculum changes that benefited their students. Due to our origins, respect for teacher expertise and agency is deeply embedded within the design of our lessons and materials.

Our website is easy to navigate, with classroom-ready lesson materials that are freely downloadable. Materials are provided in non-editable (e.g. pdf) and editable (e.g. Word) formats, to allow for easy teacher customization. Teacher notes, strategies, and pedagogical tips are provided in supplementary sections, which keep the main student-facing materials easy to digest, print, and use.